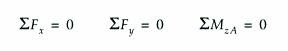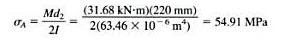Flexion

Diagrama de cortante y momento flexionante en vigas estaticamente determinadas.

Las vigas pueden clasificase en estaticamente deterninadas y estaticamnete indeterminadas. Cuando se puedan obtener las reacciones de los appoyos a partir de las ecuaciones de Estatica solamente, la viga es estaticamente determinada. Si las fuerzas aplicadas a la viga estan limitadas a un plano, se dispone de tres ecuaciones de equilibrio para determinar las reacciones de los apoyos. Las ecuaciones son:

Donde A es un punto cualquiera del plano de carga. Asi pues, se podran determinar tres componentes de las reacciones, como maximo. Si las fuerzas aplicadas y las reacciones de los apoyos son siempre perpendiculares al eje longitudinal de la viga. Para que esa viga sea estaticamente, solo podran haber dos fuerzas reactivas incognitas, ya que el numero de ecuaciones de equilibrio de que se dispone se ha reducido a dos, las cuales son:

Son ejemplos de vigas estaticamnete determinadas las vigas simples, las sobresalientes y las mensulas. Cuando la viga tenga mas apoyos de los necesarios para mantener el equilibrio, las ecuaciones de equilibrio no son suficientes para determinar las reacciones de los apoyos. De dichas vigas se dice que son estaticamnete indeterminadas y para determinar las reacciones de los apoyos se ha de echar mano entonces de las propiedades que relacionan la carga con la deformacion de la viga, admas de las ecuaciones de equilibrio.

Diagramas de fuerza cortante y momento flector para las vigas indicadas.

Bibliografia

Ingenieria Mecanica Estatica
Willian F. Riley
Leroy D. Sturges
Editorial Reverte, S. A.

Estatica para Ingenieros Civiles Diagramas de fuerza cortante y momento flector
Carlos Ramiro Vallecia Bahena
Universidad Santo Tomas
Consejo Editorial

Esfuerzo normal y cortante en vigas

Consideremos una viga recta con un plano de simetria y para la cual las fuerzas aplicadas son simetricas con respecto a este plano que tomaremos como plano de la figura:

Sea (S) una seccion recta de esta viga. Recordemos que esta viga esta aislada en el espacio y sometida a las fuerzas directamente aplicadas y a las reacciones de apoyo.

Se llama momento flector M, para una seccion (S), ala suma de los momentos, con respecto a un punto cualquiera de esta seccion, de las fuerzas situadas a la izquierda de (S); estas fuerzas comprenden las aplicadas directamente y las reacciones de apoyo situadas a la izquierda de (S).

Asi, para la viga apoyada en dos apoyos simples y representada en la figura de abajo, tendremos, teniendo en cuenta las convenciones de signos relativos a los momentos:

Si existiera un momento de empotramiento en A y una componente horizontal para la reaccion de apoyo seria necesario naturalmente tenerlos en cuenta en el calculo. Sin embargo, en lo que concierne a la componente horizontal HA, normalmente pasa por el punto con respecto al cual se toma el momento.

El ejemplo considerado muestra que el momento flector M varia con la abscisa de la seccion. La curva que representa el valor de M en funcion de x se denomina diagrama de momentos flectores.

Se llama esfuerzo normal N, para una seccion (S), a la suma de las proyecciones de las fuerzas situadas a la izquierda de (S) sobre la normal a esta seccion. Como en el caso precedente, las fuerzas a considerar comprenden las fuerzas directamente aplicadas y las reacciones de apoyo situadas a la izquierda de (S).

Asi para la viga representada en la figura y sometida a una carga p que tiene por componentes V y H y cuya componente horizontal  HA de la seccion de apoyo en A tiene como valor HA = H, tendremos:

-Para una seccion (S) comprendida entre A y C :  N=HA=H

-Para una seccion (S) comprendida entre C y B :  N=HA-H=0

Se llama esfuerzo cortante T, para una seccion (S), a la suma de las proyecciones de las fuerzas situadas a la izquierda de (S) sobre el plano de la seccion. Como siempre las fuerzas a considerar comprenden las fuerzas directamente aplicadas y las reacciones de apoyos. Asi tenemos:

T = VA - P1 - P2

El sistema de fuerzas externas que actuan a la izquierda de una seccion (S), podria reducirse con respecto a un punto O cualquiera del eje de simetria de esta seccion:

- A una fuerza Re, igual a la resultante de las fuerzas externas situadas a la izquierda de (S) y que puede descomponerse segun He normal a la seccion Ve en el plano de la seccion.

-Y un par de momento Me igual a la suma de los momentos, con respecto al punto O, de las fuarzas exteriore situadas a la izquierda de (S).

En estas condiciones, vemos que:

M = Me   N = He    T = Ve

es decir que M, N y T son los elementos de reduccion, con respecto al punto O, de las fuerzas aplicadas y de las reacciones de apoyi situadas a la izquierda de (S).

Bibliografia

Como Evitar los Errores en los Proyectos de Hormigon Armado

Pierre Charon

Editores Tencnicos Asociados, S. A. Barcelona

Deflexion en Vigas

Las cargas de flexion aplicadas a una viga hacen que se flexione en una direccion perpendicular a su eje. Una viga recta en su origen se deformara y su forma sera ligeramente curva. En la mayor parte de los casos, el factor critico es la deflexion maxima de la viga, o su deflexion en determinados lugares.

Considere el reductor de velocidad, con doble reduccion. Los cuatro engranes (A,B,C y D) se montan en tres ejes, cada uno de los cuales esta soportado por dos cojinetes. La accion de los engranes al transmitir potencia crea un conjunto de fuerzas, que a su vez actuan sobre los ejes y causan flexion en ellos. Un componente da la fuerza total sobre los dientes del engrane actua en una direccion que tiende a separar los dos engranes. Asi, la rueda A es impulsada hacia arriba, mientras que la rueda B es implusada hacia abajo. Para que los engranes funcionen bien, la deflexion neta de uno en relacion con el otro no debe ser mayor que 0.0015 pulg. (0.013 mm), si el engrane es industrial de tamaño mediano.

Para evaluar el diseño, existen muchos metodos para calcular las deflexiones de los ejes. Es util contar con un conjunto de formulas para calcular la deflexion de vigas, en cualquier punto o en puntos determinados, en muchos problemas practicos.

Para muchos casos adicionales, la superposicion es util si la carga realse divide en partes que se puedan calcular con las formulas ya disponibles. La deflexion para cada carga se calcula por separado y a continuacion se suman las deflexiones individuales en los puntos de interes.

Muchos programas comerciales para computadora permiten modelar las vigas que tengan puntas de carga muy complicadas y geometria variable. Entre los resultados, estan las fuerzas de reaccion, los diagramas de fuerza cortante y momento flexionante, y las deflexiones en cualquier punto. Es importante que comprenda las bases de la deflexion de las vigas.

Ejemplo:

  

Para los engranes A y B de la figura, calcule la deflexion relativa entre ellos, en el plano del papel, debido a las fuerzas que se muestran en la parte (c). Se acostumbra considerar que las cargas en los engranes, y las reacciones en los cojinetes, estan concentradas. Los ejes de los engranes son de acero y sus diametros son uniformes, con los valores que se listan en la figura.

Solucion:

Objetivo: Calcular la deflexion relativa entre los engranes A y B de la figura.

Datos:

Resultados:

Los principios generales que relacionan la deflexion de una viga con la forma en que esta cargada y la forma en que esta apoyada se presentaran a continuacion. El resultado sera un conjunto de relaciones entre la carga, la fuerza cortante vertical, el momento de flexion, la pendiente de la viga flexionada y la curva de la deflexion real e la viga.

Un concepto fundamental para las vigas en flexion es:

Las ultimas dos ecuaciones son consecuencia de la obsevacion de que existe una realcion de derivada (Pendiente) entre el cortante y el momento flexionante, y entre la carga y el corte.

En la practica, las ecuaciones fundamentales que se acaban de citar se usan en forma inversa. Esto es, se conoce la distribucion de carga en funcion de x, y las ecuaciones para los demas factores se deducen por integraciones sucesivas. Los resultados son:

En muchos casos, se pueden trazar los diagramas de carga, fuerza cortante y momento de flexion, en la forma convencional, y las ecuaciones de la fuerza cortante o del momento de flexion se pueden deducir en forma directa con los principios de la geometria analitica. Con M en funcion de x, se pueden determinar las relaciones de pendiente y deflexion:

Las constantes de integracion deben evaluarse a partir de las condiciones de frontera.


Bibliografia
Diseño de Elementos de Maquinas
Cuarta Edicion
Robert. L. Mott, P. E.
Editorial Pearson Education

Vigas estaticamente indeterminadas

Tal como se ha visto en el caso de las vigas tambien surgen situaciones estaticamente indeterminadas (Mayor numero de reacciones que ecuaciones, por lo que debera obtenerse apartir de las deformaciones, ecuaciones adicionales que levanten la indeterminacion).

Pero como surgen las vigas estaticamente indeterminadas? Veamos:

La siguiente viga es estaticamente determinada:

Al hacer el analisis deben calcularse los esfuerzos actuantes maximos y la deformacion maxima.

Estos valores deben ser menores que los esfuerzos y la deformacion admisibles para que la viga sea segura y funcional. Sin embargo puede suceder que sean mayores (uni de ellos o todos).

En este caso el diseñador debe enfrentar varias alternativas:

a) Cambiar el material (por uno mas resistente o mas rigido segun el caso).

b) Aumentar la seccion transversal de la viga incrementando su resistencia y su rigidez, sin cambiar el material.

Sin embargo en muchas ocaciones no es posible cambiar el material o las dimenciones por problemas de disponibilidad de otros materiales o por requerimientos arquitectonicos que no hacen posible cambiar las dimensiones.

En estas condiciones la unica alternativa para aumentar la seguridad de la viga y su rigidez sera colocar un apoyo adicional intermedio C.

Esta es otra de la ventajas de las vigas estaticamente indeterminadas: Los apoyos redundantes garantisan la estabilidad en caso de fallas. En general, mientras mas apoyos redundantes tenga una viga o estructura, mas segura sera. Logicamente tambien tendra un mayor grado de indeterminacion y por consiguiente el analisis sera mas largo, puesto que involucrara mas ecuaciones.

Observemos como se obtiene la ecuacion adicional que nos resuelve la indeterminacion:

 

Para resolver el problema empleamos un artificio muy utilizado en ingenieria estructural: Quitamos el apoyo redundante y dejamos que la viga se deforme, luego lo volvemos a poner a actuar revirtiendo la deformacion que obviamente sera igual a la primera. Para el analisis empleamos el principio de superposicion asi:

Como en la situacion original hay un apoyo en C, alli la deformacion sera cero. Por este motivo:

Bibliografia:
Resistencia de Materiales Basica para Estudiantes de Ingenieria
Jorge Eduardo Salazar Trujillo
Universida Nacional de Colombia 
Sede Manizales 

Esfuerzos combinados

Circulo de Mohr para esfuerzos

Obtencion de los esfuerzos principales

Supongase que el plano inclinado cuya normal es N es un plano principal. Definiendo S como la magnitud de esfuerzo principal que actua sobre un plano vertical cuyos cosenos directos son l, m, n. Se obtiene:

Para la solucion de este sistema notese que la solucion trivial  m=n=l=0 es inaceptable pues se sabe que:

Para que el sistema presentado en las ecuaciones sea homogeneo y tenga soluciones diferentes de cero, el determinante del mismo debe ser cero.

O sea:



Efectuando el determinante se obtiene:

Invariante de esfuerzos

Sean:

Sin embargo sustituyendo en (b) las ecuaciones se obtiene:

Las tres raices de S son los valores de los esfuerzos principales.

Esfuerzo Cortante Maximo

Sean 1, 2, 3, los ejes principales de un plano dado, en modo tal que los esfuerzos x, y, z, se convierten en esfuerzos principales. Entonces:

El cuadrado del esfuerzo cortante que actua sobre el plano principal es:

Tendremos entonces que:

Notese que "l" o "m" deben ser cero ya que las expresiones entre parentesis son diferentes de cero.

Recordando la ecuacion (e) y sustituyendo los valores de los cosenos directores indicados en la tabla anterior se obtiene los siguientes esfuerzos cortantes:

 Circulo de Mohr. Estado tridimensional de Esfuerzos:

Observaciones

1) Se puede mostrar que para cualquier valor de los cosenos directores m, n, y l el estado de esfuerzos estara representado por la zona achurada del Circulo de Mohr.

2) No es posible encontrar mediante el Circulo de Mohr las direcciones pricipales ni el valor de los esfuerzos pricipales en el caso del estado de esfuerzos en el espacio. Para el calculo de los esfuerzos principales, se deduce que es necesario resolver una ecuacion cubica que no se puede representar mediante el Circulo de Mohr. Las ecuaciones de transformacion de esfuerzos pueden deducirse del circulo de Mohr solo en caso del estado de esfuerzo en plano. El Circulo de Mohr encuentra su aplicacion en el caso de los esfuerzos en el espacio cuando estos son principales.

Bibliografia

El Circulo de Mohr Fundamentos y Aplicaciones

Carlos Ramiro Vallecilla Bahena

Universidad Santo Tomas

Consejo Editorial

Analisis de esfuerzo bajo cargas combinadas

A menudo es posible analizar un miembro estructural sometido a cargas combinadas superponiendo los esfuerzos y deformaciones causados por cada carga que actua por separado. Ahora bien, la superposicion de los esfuerzos y las deformaciones es permisible solo en ciertas condiciones. Un requisito es que los esfuerzos y las defomaciones deben ser funciones lineales de las cargas aplicadas. Esto requiere a su vez que el material obedezca la ley de Hooke y que los desplazamientos sean pequeños.

Otro requisito es que no debe existir interaccion entre las diversas cargas; es decir, los esfuerzos y deformaciones causados por una de las cragas no deben verse afectados por la presencia de otras cargas. La mayor parte de las estructuras comunes satisfacen estas dos condiciones, por lo que el uso de la superposicion es muy comun en el trabajo ingenieril.

Si bien hay muchas maneras de analizar una estructura sometida a mas de un tipo de carga, por lo general el procedimiento incluye los siguientes pasos:

1.- Se elige un punto en la estructura para determinar los esfuerzos y las deformaciones (Por lo general se escoje un punto en una seccion transversal, donde los esfuerzos son grandes; por ejemplo, en una seccion transversal, donde el momento flexionante tiene su valor maximo).

2.- Para cada carga sobre la estructura se determinan las resultantes de esfuerzo en la seccion transversal que contenga el punto seleccionado (Las posibles resultantes de los esfuerzos son una fuerxa axial, un momento de torsion, un momento flexionante y una fuerza cortante).

3.- Se calculan los esfuerzos normal y cortante en el punto seleccionado debidos a cada una de las resultantes de esfuerzos. Ademas si la estructura es un recipiente a presion, determinar los esfuerzos debidos a la presion interna.

El procedimiento descrito para analizar los esfuerzos en los puntos A y B, puede usarse en otros puntos. Los puntos donde los esfuerzos calculados con la formula de flexion y las formulas de los cortantes tienen valores maximos y minimos, llamados puntos criticos, los esfuerzos normales debidos a la flexion son maximos en la secci transversal de momento flexionante maximo que se presenta en el soporte, por tanto, los puntos en las partes superior e inferior de la viga en el extremo empotrado son los puntos criticos para el calculo de los esfuerzos.

Como paso final, los esfuerzos principales y los esfuerzos cortantes maximos en los puntos criticos pueden compararse entre si para determinar los esfuerzos normales y cortantes maximos absolutos en la barra. Con la variedad de situaciones practicas no parece tener limite, no vale la pena obtener formulas especificas para calcular los esfuerzos maximos. Cada estructura suele tratarse como caso especial.

Seleccion de los puntos criticos

Si el objetivo del analisis es determinar los esfuerzos maximos en cualquier parte de la estructura, entonces hay que escoger lso puntos criticos en secciones transversales donde las resultantes de esfuerzos alcancen los valores maximos. Ya en dichas secciones se elegiran los puntos en que los esfuerzos normales o los esfuerzos cortantes tengan sus valores maximos. Si la seleccion de los puntos se hace con buen juicio, podremos estar razonablemente seguros de haber obtenido los esfuerzos maximos en la estructura. Sin embargo, a veces es dificil reconocer de ante mano donde se localizan los esfuerzos maximos en el miembro. Entonces quiza sea necesario investigar los esfuerzos en un  gran numero de puntos. Otras estrategias tambien pueden resultar utiles, como obtener ecuaciones especificas para el problema en conosideracion o alaborar hipotesis simplificadoras a fin de facilitar un analisis que podria resultar sumamente dificil sin ellas.      

 Ejemplo: Un poste circular hueco con diametro exterior de 220 mm y diametro interior de 180 mm sostiene un letrero de dimensiones de 2.0 m x 1.2 m. El letrero esta desplazado 0.5 m del centro del poste y su borde inferior esta 6.0 m sobre el terreno. 

Solucion

La presion del viento contra el letrero produce una fuerza resultante W que actua en el punto medio de este y es igual a la presion p multiplicada por el area A sobre la que actua:

  

 

La linea de accion de esta fuerza esta a una altura h = 6.6 m sobre el suelo y uan distancia b = 1.5 m de la linea central del poste. La fuerza del viento que actua sobre el letrero es estaticamente equivalente a una fuerza lateral W y a un par de torsion T que actua sobre el poste. El par es igual a la fuerza W multiplicada por la distancia b:

Las resultantes de esfuerzos en la base del poste son un momento flexionante M, un par de torsion T y una fuerza cortante V. Sus magnitides son: 

El examen de esta resultantes de esfuerzos muestra que los esfuerzos de flexion maximos ocurren con el punto A y los esfuerzos cortantes maximos con el punto B; Por tanto A y B son puntos criticos donde deben determinarse los esfuerzos .

Esfuerzos en el los puntos A y B. El momento flexionante M produce un esfuerzo de tension en el punto A pero ningun esfuerzo en el punto B. El esfuerzo de tension en el punto A se obtiene con la formula de flexion: 

 Donde d2 es el diametro exterior (220 mm) e I es el momento de inercia de la seccion transversal. El momento de inersia es:

 Donde d1 es el diametro interior. Por la tanto el esfuerzo de tension en el punto A es.

 El par de torsion T produce esfuerzos cortantes, en los puntos A y B. Podemos calcular dichos esfuerzos con la formula de torsion:

donde Ip es el momento polar de inercia:

Entonces

Por ultimo calculamos los esfuerzos cortantes en los puntos A y B debidos a la fuerza cortante V. el esfuerzo cortante en el punto A es cero y el esfuerzo cortante en el punto B se obtiene con la formula del cortante para un tubo circular :

ecu (j)

Donde r2 y r1 son los radios exterior e interior, respectivamente, y A es el area de la seccion transversal:

Al sustituir los valores numericos en la ecu (j), obtenemos:

Ahora hemos calculado todos los esfuerzos que actuan sobre los puntos A y B de la seccion transversal.

Elementos de esfuerzo. El siguiente paso es mostrar estos esfuerzos sobre elementos de esfuerzo. Para ambos elementos, el eje "y" es paralelo al eje longitudinal del poste y el eje x es horizontal. En el punto A, los esfuerzos que actuan sobre el elementos son

 En el punto B, los esfuerzos son

Puesto que no existen esfuerzos normales que esten actuando sobre el elemento, en el punto B se encuentra en estado de cortante puro. Ahora que conocemos todos los esfuerzos que actuan sobre los elementos de esfuerzo, podemos usar las ecuaciones para determinar los esfuerzos principales y los esfuerzos cortantes maximos.

Esfuerzos principales y  esfuerzos cortantes maximos en el punto A. Los esfuerzos principales se obtienen con la ecuacion: 

sustituimos

Los esfuerzos maximos en el plano pueden obtenerse con la ecuacion

Este termino se evaluo antes, por lo que vemos de inmediato que

Puesto que los esfuerzos principales tiene signos opuestos, los esfuerzos cortantes maximos en el plano son mayores que los esfuersos cortantes maximos en el plano son mayores que los esfuerzos cortantes maximos fuera del plano; por tanto, el esfuerzo cortante maximo en el punto A es de 28.2Mpa.

Esfuerzos principales y esfuerzos cortantes en el punto B. Los esfuerzos en este punto son 

Dado que el elemento esta en estado cortante puro, los esfuerzos principales son 

y el esfuerzo cortante maximo en el plano es

Los esfuerzos cortantes maximos fuera del plano tienen la mitad de este valor.

Nota: Si se requieren los esfuerzos maximos en cualquier parte del poste, hay que determinar tambien los esfuerzos en el punto critico diametralmente opuesto al punto A, por uqe en dicho punto el esfuerzo de compresion debido a la flexion alcanza el valor maximo. Los esfuerzos principales en ese punto son

y el esfuerzo cortante maximo es de 28.2 MPa; por tanto, el esfuerzo de tension maximo en el poste es de 55.7 MPa, el esfuerzo maximo de compresion es de -55.7 MPa y el esfuerzo cortante maximo es de 28.2 MPa (Recuerde que solo se han considerado los efectos de la presion del viento en el analisis. Otras cargas, como el peso de la estructura, tambien producen esfuerzos en la base del poste).

Bibliografia

Mecanica de Materiales

James M Gere

Editorial Thomson

Sexta edicion