 A menudo es posible analizar un miembro estructural sometido a cargas combinadas superponiendo los esfuerzos y deformaciones causados por cada carga que actua por separado. Ahora bien, la superposicion de los esfuerzos y las deformaciones es permisible solo en ciertas condiciones. Un requisito es que los esfuerzos y las defomaciones deben ser funciones lineales de las cargas aplicadas. Esto requiere a su vez que el material obedezca la ley de Hooke y que los desplazamientos sean pequeños.
A menudo es posible analizar un miembro estructural sometido a cargas combinadas superponiendo los esfuerzos y deformaciones causados por cada carga que actua por separado. Ahora bien, la superposicion de los esfuerzos y las deformaciones es permisible solo en ciertas condiciones. Un requisito es que los esfuerzos y las defomaciones deben ser funciones lineales de las cargas aplicadas. Esto requiere a su vez que el material obedezca la ley de Hooke y que los desplazamientos sean pequeños.Otro requisito es que no debe existir interaccion entre las diversas cargas; es decir, los esfuerzos y deformaciones causados por una de las cragas no deben verse afectados por la presencia de otras cargas. La mayor parte de las estructuras comunes satisfacen estas dos condiciones, por lo que el uso de la superposicion es muy comun en el trabajo ingenieril.
Si bien hay muchas maneras de analizar una estructura sometida a mas de un tipo de carga, por lo general el procedimiento incluye los siguientes pasos:
1.- Se elige un punto en la estructura para determinar los esfuerzos y las deformaciones (Por lo general se escoje un punto en una seccion transversal, donde los esfuerzos son grandes; por ejemplo, en una seccion transversal, donde el momento flexionante tiene su valor maximo).
2.- Para cada carga sobre la estructura se determinan las resultantes de esfuerzo en la seccion transversal que contenga el punto seleccionado (Las posibles resultantes de los esfuerzos son una fuerxa axial, un momento de torsion, un momento flexionante y una fuerza cortante).
3.- Se calculan los esfuerzos normal y cortante en el punto seleccionado debidos a cada una de las resultantes de esfuerzos. Ademas si la estructura es un recipiente a presion, determinar los esfuerzos debidos a la presion interna.
El procedimiento descrito para analizar los esfuerzos en los puntos A y B, puede usarse en otros puntos. Los puntos donde los esfuerzos calculados con la formula de flexion y las formulas de los cortantes tienen valores maximos y minimos, llamados puntos criticos, los esfuerzos normales debidos a la flexion son maximos en la secci transversal de momento flexionante maximo que se presenta en el soporte, por tanto, los puntos en las partes superior e inferior de la viga en el extremo empotrado son los puntos criticos para el calculo de los esfuerzos.
Como paso final, los esfuerzos principales y los esfuerzos cortantes maximos en los puntos criticos pueden compararse entre si para determinar los esfuerzos normales y cortantes maximos absolutos en la barra. Con la variedad de situaciones practicas no parece tener limite, no vale la pena obtener formulas especificas para calcular los esfuerzos maximos. Cada estructura suele tratarse como caso especial.
Seleccion de los puntos criticos
 Si el objetivo del analisis es determinar los esfuerzos maximos en cualquier parte de la estructura, entonces hay que escoger lso puntos criticos en secciones transversales donde las resultantes de esfuerzos alcancen los valores maximos. Ya en dichas secciones se elegiran los puntos en que los esfuerzos normales o los esfuerzos cortantes tengan sus valores maximos. Si la seleccion de los puntos se hace con buen juicio, podremos estar razonablemente seguros de haber obtenido los esfuerzos maximos en la estructura. Sin embargo, a veces es dificil reconocer de ante mano donde se localizan los esfuerzos maximos en el miembro. Entonces quiza sea necesario investigar los esfuerzos en un gran numero de puntos. Otras estrategias tambien pueden resultar utiles, como obtener ecuaciones especificas para el problema en conosideracion o alaborar hipotesis simplificadoras a fin de facilitar un analisis que podria resultar sumamente dificil sin ellas.
Si el objetivo del analisis es determinar los esfuerzos maximos en cualquier parte de la estructura, entonces hay que escoger lso puntos criticos en secciones transversales donde las resultantes de esfuerzos alcancen los valores maximos. Ya en dichas secciones se elegiran los puntos en que los esfuerzos normales o los esfuerzos cortantes tengan sus valores maximos. Si la seleccion de los puntos se hace con buen juicio, podremos estar razonablemente seguros de haber obtenido los esfuerzos maximos en la estructura. Sin embargo, a veces es dificil reconocer de ante mano donde se localizan los esfuerzos maximos en el miembro. Entonces quiza sea necesario investigar los esfuerzos en un gran numero de puntos. Otras estrategias tambien pueden resultar utiles, como obtener ecuaciones especificas para el problema en conosideracion o alaborar hipotesis simplificadoras a fin de facilitar un analisis que podria resultar sumamente dificil sin ellas. Ejemplo: Un poste circular hueco con diametro exterior de 220 mm y diametro interior de 180 mm sostiene un letrero de dimensiones de 2.0 m x 1.2 m. El letrero esta desplazado 0.5 m del centro del poste y su borde inferior esta 6.0 m sobre el terreno.
Solucion
La presion del viento contra el letrero produce una fuerza resultante W que actua en el punto medio de este y es igual a la presion p multiplicada por el area A sobre la que actua:
La linea de accion de esta fuerza esta a una altura h = 6.6 m sobre el suelo y uan distancia b = 1.5 m de la linea central del poste. La fuerza del viento que actua sobre el letrero es estaticamente equivalente a una fuerza lateral W y a un par de torsion T que actua sobre el poste. El par es igual a la fuerza W multiplicada por la distancia b:
Las resultantes de esfuerzos en la base del poste son un momento flexionante M, un par de torsion T y una fuerza cortante V. Sus magnitides son:
La linea de accion de esta fuerza esta a una altura h = 6.6 m sobre el suelo y uan distancia b = 1.5 m de la linea central del poste. La fuerza del viento que actua sobre el letrero es estaticamente equivalente a una fuerza lateral W y a un par de torsion T que actua sobre el poste. El par es igual a la fuerza W multiplicada por la distancia b:
Las resultantes de esfuerzos en la base del poste son un momento flexionante M, un par de torsion T y una fuerza cortante V. Sus magnitides son:
El examen de esta resultantes de esfuerzos muestra que los esfuerzos de flexion maximos ocurren con el punto A y los esfuerzos cortantes maximos con el punto B; Por tanto A y B son puntos criticos donde deben determinarse los esfuerzos .
Esfuerzos en el los puntos A y B. El momento flexionante M produce un esfuerzo de tension en el punto A pero ningun esfuerzo en el punto B. El esfuerzo de tension en el punto A se obtiene con la formula de flexion:
Donde d2 es el diametro exterior (220 mm) e I es el momento de inercia de la seccion transversal. El momento de inersia es:
Donde d1 es el diametro interior. Por la tanto el esfuerzo de tension en el punto A es.
El par de torsion T produce esfuerzos cortantes, en los puntos A y B. Podemos calcular dichos esfuerzos con la formula de torsion:
donde Ip es el momento polar de inercia:
Entonces
Por ultimo calculamos los esfuerzos cortantes en los puntos A y B debidos a la fuerza cortante V. el esfuerzo cortante en el punto A es cero y el esfuerzo cortante en el punto B se obtiene con la formula del cortante para un tubo circular :
Donde r2 y r1 son los radios exterior e interior, respectivamente, y A es el area de la seccion transversal:
Al sustituir los valores numericos en la ecu (j), obtenemos:
Ahora hemos calculado todos los esfuerzos que actuan sobre los puntos A y B de la seccion transversal.
Elementos de esfuerzo. El siguiente paso es mostrar estos esfuerzos sobre elementos de esfuerzo. Para ambos elementos, el eje "y" es paralelo al eje longitudinal del poste y el eje x es horizontal. En el punto A, los esfuerzos que actuan sobre el elementos son
En el punto B, los esfuerzos son
Puesto que no existen esfuerzos normales que esten actuando sobre el elemento, en el punto B se encuentra en estado de cortante puro. Ahora que conocemos todos los esfuerzos que actuan sobre los elementos de esfuerzo, podemos usar las ecuaciones para determinar los esfuerzos principales y los esfuerzos cortantes maximos.
Esfuerzos principales y esfuerzos cortantes maximos en el punto A. Los esfuerzos principales se obtienen con la ecuacion:
sustituimos
Los esfuerzos maximos en el plano pueden obtenerse con la ecuacion
Este termino se evaluo antes, por lo que vemos de inmediato que
Puesto que los esfuerzos principales tiene signos opuestos, los esfuerzos cortantes maximos en el plano son mayores que los esfuersos cortantes maximos en el plano son mayores que los esfuerzos cortantes maximos fuera del plano; por tanto, el esfuerzo cortante maximo en el punto A es de 28.2Mpa.
Esfuerzos principales y esfuerzos cortantes en el punto B. Los esfuerzos en este punto son
Dado que el elemento esta en estado cortante puro, los esfuerzos principales son
y el esfuerzo cortante maximo en el plano es
Los esfuerzos cortantes maximos fuera del plano tienen la mitad de este valor.
Nota: Si se requieren los esfuerzos maximos en cualquier parte del poste, hay que determinar tambien los esfuerzos en el punto critico diametralmente opuesto al punto A, por uqe en dicho punto el esfuerzo de compresion debido a la flexion alcanza el valor maximo. Los esfuerzos principales en ese punto son
y el esfuerzo cortante maximo es de 28.2 MPa; por tanto, el esfuerzo de tension maximo en el poste es de 55.7 MPa, el esfuerzo maximo de compresion es de -55.7 MPa y el esfuerzo cortante maximo es de 28.2 MPa (Recuerde que solo se han considerado los efectos de la presion del viento en el analisis. Otras cargas, como el peso de la estructura, tambien producen esfuerzos en la base del poste).
Bibliografia
Mecanica de Materiales
James M Gere
Editorial Thomson
Sexta edicion





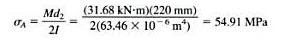















Este comentario ha sido eliminado por el autor.
ResponderEliminarel primer comentario decía todos los errores del problema, el autor lo elimino...
Eliminar