Las vigas pueden clasificase en estaticamente deterninadas y estaticamnete indeterminadas. Cuando se puedan obtener las reacciones de los appoyos a partir de las ecuaciones de Estatica solamente, la viga es estaticamente determinada. Si las fuerzas aplicadas a la viga estan limitadas a un plano, se dispone de tres ecuaciones de equilibrio para determinar las reacciones de los apoyos. Las ecuaciones son:
Donde A es un punto cualquiera del plano de carga. Asi pues, se podran determinar tres componentes de las reacciones, como maximo. Si las fuerzas aplicadas y las reacciones de los apoyos son siempre perpendiculares al eje longitudinal de la viga. Para que esa viga sea estaticamente, solo podran haber dos fuerzas reactivas incognitas, ya que el numero de ecuaciones de equilibrio de que se dispone se ha reducido a dos, las cuales son:
Son ejemplos de vigas estaticamnete determinadas las vigas simples, las sobresalientes y las mensulas. Cuando la viga tenga mas apoyos de los necesarios para mantener el equilibrio, las ecuaciones de equilibrio no son suficientes para determinar las reacciones de los apoyos. De dichas vigas se dice que son estaticamnete indeterminadas y para determinar las reacciones de los apoyos se ha de echar mano entonces de las propiedades que relacionan la carga con la deformacion de la viga, admas de las ecuaciones de equilibrio.
Diagramas de fuerza cortante y momento flector para las vigas indicadas.
Bibliografia
Ingenieria Mecanica EstaticaWillian F. Riley
Leroy D. Sturges
Editorial Reverte, S. A.
Estatica para Ingenieros Civiles Diagramas de fuerza cortante y momento flector
Carlos Ramiro Vallecia Bahena
Universidad Santo Tomas
Consejo Editorial
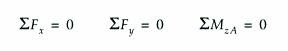







Ma vie est belle grâce à vous, Mein Helfer. Seigneur Jésus dans ma vie comme une lumière de bougie dans l'obscurité. Tu m'as montré le sens de la foi avec tes paroles. Je sais que même lorsque je pleurais toute la journée en pensant à la façon de me rétablir, tu ne dormais pas, tu m'étais cher. J'ai contacté le centre d'herboristerie Dr Itua, qui vivait en Afrique de l'Ouest. Un de mes amis, ici à Hambourg, est également originaire d'Afrique. Elle m'a parlé des herbes africaines, mais j'étais nerveux. J'ai très peur quand il s'agit de l'Afrique parce que j'ai entendu beaucoup de choses terribles à leur sujet à cause de mon christianisme. Dieu pour la direction, faites un pas audacieux et prenez contact avec lui dans le courriel et puis allez à WhatsApp, il m'a demandé si je peux venir pour un traitement ou si je veux une livraison, je lui ai dit que je voulais le connaître j'achète des billets d'avion de 2 façons pour l'Afrique Pour rencontrer le Dr Itua, je suis allé là-bas et j'étais sans voix de la part des gens que j'y ai vu. Brevet, des gens malades. Itua est un dieu envoyé dans le monde, j'ai parlé à mon pasteur de ce que je fais, le pasteur Bill Scheer. Nous avons une belle bataille avec l'esprit et la chair. Adoration la même nuit. Il a prié pour moi et m'a demandé de diriger. J'ai passé 2 semaines et 2 jours en Afrique au Dr Itua Herbal Home. Après le traitement, il m'a demandé de rencontrer son infirmière pour faire le test du VIH quand je l'aurais fait. Il était négatif. J'ai demandé à mon ami de m'emmener dans un autre hôpital voisin quand je suis arrivé, il était négatif. Le résultat m'a fait perdre la tête, mais j'étais heureuse au fond de moi. Nous sommes allés avec le Dr Itua, je le remercie mais je lui explique que je n'ai pas assez pour lui montrer ma reconnaissance, qu'il comprend ma situation, mais je lui promets qu'il témoignera de son bon travail. Dieu merci pour ma chère amie Emma, je sais que je pourrais lire ceci maintenant, je veux vous remercier. Et un grand merci au Dr. Itua Herbal Center. Il m'a donné son calendrier que j'ai accroché au mur de ma maison. Le Dr Itua peut également soigner les maladies suivantes : VIH, herpès, hépatite B, foie inflammatoire, diabète, cancer de la vessie, cancer du cerveau, cancer de l'œsophage, cancer de la vésicule biliaire, maladie trophoblastique gestationnelle, cancer de la tête et du cou, lymphome de Hodgkin
ResponderEliminarCancer de l'intestin,Cancer du rein,Leucémie,Cancer du foie,Cancer du poumon,Mélanome,Mésothéliome,Myélome multiple,Tumeurs neuroendocriniennes
Lymphome non hodgkinien,Cancer de la bouche,Cancer de l'ovaire,Cancer du sinus,Cancer de la peau,Sarcome des tissus mous,Cancer de la colonne vertébrale,Cancer de l'estomac
Cancer du testicule,Cancer de la gorge,Cancer de la thyroïde,Cancer de l'utérus,Cancer du vagin,Cancer de la vulveDésordre bipolaire,Cancer de la vessie,Cancer colorectal,HPV,Cancer du sein,Cancer de l'anus.Appendice.,Cancer du rein,Cancer de la prostate,Glaucome.., Cataractes,Dégénérescence maculaire,Cancer des surrénales.cancer des voies biliaires,Cancer des os.maladie cardiovasculaire,maladie pulmonaire.hypertrophie de la prostate,ostéoporoseAlzheimer,cancer du cerveau.démence.érection faible,période d'amour,leucémie,fribroïde,stérilité,maladie de Parkinson,maladie inflammatoire de l'intestin ,fibromyalgie, récupérer votre ex. Vous pouvez le contacter par e-mail ou drituaherbalcenter@gmail.com, ..numéro de téléphone de WhatsApp + 2348149277967 ... C'est un bon médecin, parlez-lui gentiment. Je suis sûr qu'il vous écoutera aussi.